ワタタク今回の記事の目的はProcessingの「sin()関数」を理解し、自分なりに使ってみること。
【Processing】sin()関数について
- sinは英語でsineという
- 角度の大きさに対応する二次元平面上の点のy座標を表現する
- 角度を使って波のような形を作る関数
- 波の上下の動きもつくることができる
sin()関数を使うときの注意点は、角度がラジアン（radian）であること- ラジアンは度数（degree）と違うので、計算するときに変換が必要
【Processing】sin()関数の書き方【構文】
- sin(angle)
- angleはラジアン（数値）
【Processing】sin()関数の使い方【画像とコード】
/*
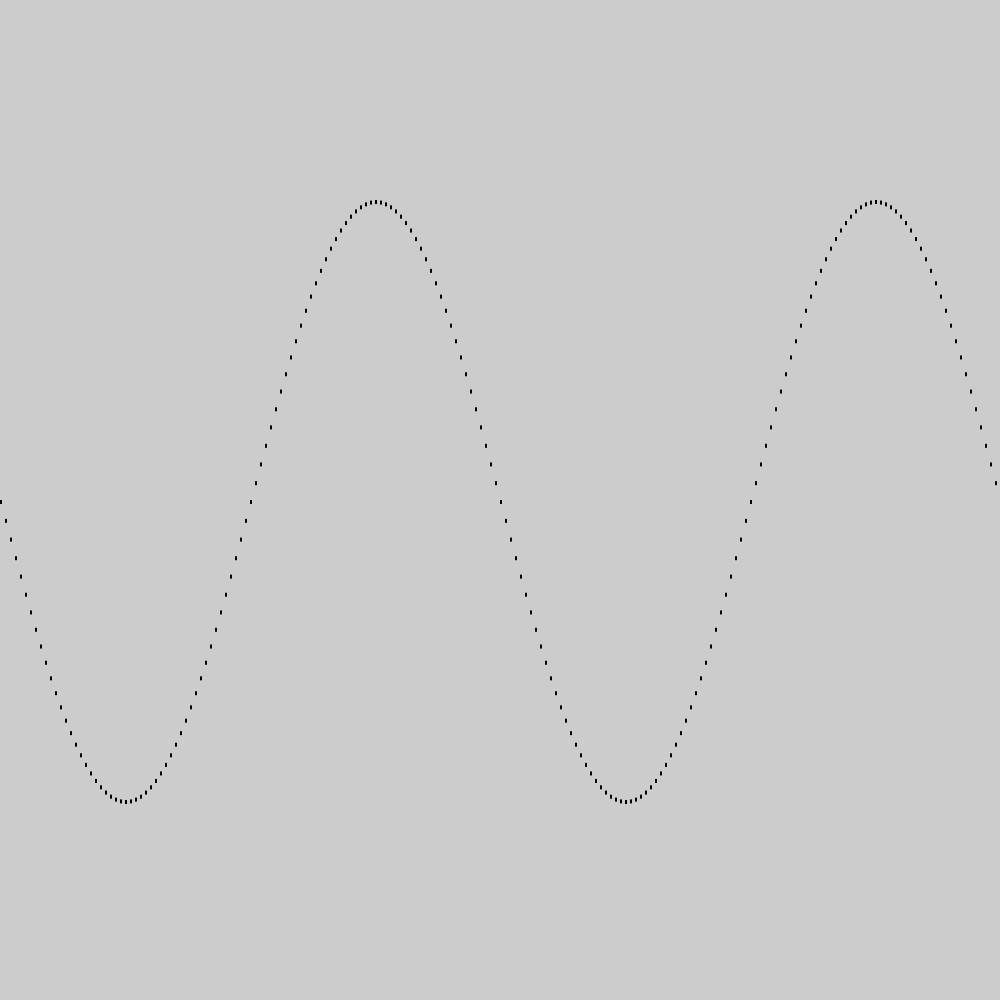
Processing ビジュアルデザイナーとアーティストのためのプログラミング入門
292ページ20-34の例題を少し変更して、僕が調べた初心者向けの解説を加える
*/
// offsetは「位置をずらす」「基準からのずれ」という意味
// 波の基本となる高さ、つまり垂直方向の基準点を決める値だよ。この値を使って、sin()関数の出力に調整を加えて、波の中心位置を上下に移動させる
// offset = 500.0;と設定すると、波の中心が画面の縦方向に500ピクセルの位置に来るようにする。
float offset = 500.0;
// scaleValは「拡大値」や「スケール値」を指している
// この例では、波の振幅を決める重要な値として使われている
float scaleVal = 300.0;
/*
float angleInc = PI/28.0;の説明
angleInc の「angle」は「角度」を、「Inc」は「increment（増加）」の略
angleIncは「角度の増分」を意味している。
PI/100.0は約3.6度 波は滑らか
PI/50.0は約7.2度
PI/20.0は約18度
PI/10.0は約36度 このコードのsizeで波ってのが分かるようになる
PI/5.0は約72度
PI/2.0は約90度
*/
float angleInc = PI/50.0;
void setup() {
size(1000, 1000);
noStroke();
fill(0);
}
// 38行目の計算式は少し先に書いています
void draw() {
background(204);
float angle = 0.0;
for (int x = 0; x < width; x += 5) {
float y = offset + (sin(angle) * scaleVal);
rect(x, y, 2, 4);
angle += angleInc;
}
}1回目と2回目のforループの処理について
1回目のforループ
1回目のforループの処理でangleは初期値の0だから、計算は以下のようになります。
y=500+(sin(0)×300)
sin(0)は0だから、
y=500+(0×300)=500
1回目のループではyは500の位置に描かれる
2回目のforループ
y=500+(sin(π/50)×300)
PI/50を計算すると約0.0628
y=500+(0.0628×300)≈500+18.84=518.84
だから、2回目のforループでのyの値は約518.84にな
これで次のポイントが描画される。
3回目のループ
y=500+(sin(2×π/50)×300)
計算すると約0.1257
y=500+(0.1257×300)≈500+37.71=537.71
だから、3回目のforループでのyの値は約537.71になる。
y=500+(sin(2×π/50)×300)はなぜ2×π/50になるのか？
- 1回目のループでは、
angleが0から始まるから、sin(0)を使う。 - ループが1回進むたびに、
angleはPI/50だけ増える。つまり、2回目のループではangleがPI/50になる。 - 3回目のループでは、さらに
PI/50だけ増えるから、angleが2×PI/50になる。
つまり、毎回少しずつ角度が増えていくことで、波の形が進んでいく。
4回目のループは以下のような計算になります。
y=500+(sin(3×π/50)×300) = 約556.49になる。
1回目から21回めまでのループの処理を表でまとめ計算式も載せる
さきほどのコードをもう1度コメントをしていない状態で載せ、forループ1回目から21回目の処理がどうなっているのか表でまとめています。
float offset = 500.0;
float scaleVal = 300.0;
float angleInc = PI/50.0;
void setup() {
size(1000, 1000);
noStroke();
fill(0);
}
void draw() {
background(204);
float angle = 0.0;
for (int x = 0; x < width; x += 5) {
float y = offset + (sin(angle) * scaleVal);
rect(x, y, 2, 4);
angle += angleInc;
}
}| ステップ | x の値 | angle の値 | sin(angle) の値 | y の計算 | y の値 |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 500 + (0 * 300) | 500 |
| 2 | 5 | PI/50 | 0.0628 | 500 + (0.0628 * 300) | 約518.84 |
| 3 | 10 | 2*PI/50 | 0.1257 | 500 + (0.1257 * 300) | 約537.71 |
| 4 | 15 | 3*PI/50 | 0.1883 | 500 + (0.1883 * 300) | 約556.49 |
| 5 | 20 | 4*PI/50 | 0.2504 | 500 + (0.2504 * 300) | 約575.12 |
| 6 | 25 | 5*PI/50 | 0.3120 | 500 + (0.3120 * 300) | 約593.60 |
| 7 | 30 | 6*PI/50 | 0.3730 | 500 + (0.3730 * 300) | 約611.90 |
| 8 | 35 | 7*PI/50 | 0.4331 | 500 + (0.4331 * 300) | 約629.93 |
| 9 | 40 | 8*PI/50 | 0.4921 | 500 + (0.4921 * 300) | 約647.63 |
| 10 | 45 | 9*PI/50 | 0.5495 | 500 + (0.5495 * 300) | 約664.86 |
| 11 | 50 | 10*PI/50 | 0.6050 | 500 + (0.6050 * 300) | 約681.50 |
| 12 | 55 | 11*PI/50 | 0.6584 | 500 + (0.6584 * 300) | 約697.53 |
| 13 | 60 | 12*PI/50 | 0.7095 | 500 + (0.7095 * 300) | 約712.85 |
| 14 | 65 | 13*PI/50 | 0.7582 | 500 + (0.7582 * 300) | 約727.46 |
| 15 | 70 | 14*PI/50 | 0.8042 | 500 + (0.8042 * 300) | 約741.26 |
| 16 | 75 | 15*PI/50 | 0.8473 | 500 + (0.8473 * 300) | 約754.19 |
| 17 | 80 | 16*PI/50 | 0.8874 | 500 + (0.8874 * 300) | 約766.21 |
| 18 | 85 | 17*PI/50 | 0.9243 | 500 + (0.9243 * 300) | 約777.29 |
| 19 | 90 | 18*PI/50 | 0.9580 | 500 + (0.9580 * 300) | 約787.40 |
| 20 | 95 | 19*PI/50 | 0.9881 | 500 + (0.9881 * 300) | 約796.43 |
| 21 | 100 | 20*PI/50 | 1.0000 | 500 + (1.0000 * 300) | 800.00 |
【Processing】sin()関数はなぜ波を描けるのか
sin()関数が波線になるのは、サイン関数が角度（ラジアン）に対して繰り返しのパターンを持っているからです。もっと簡単に言うと、サイン関数は周期的な波の形を作ることができるんです。
例えば、0度から360度までの角度を考えると、その間にサインの値は0から1へ、1から0へ、0から-1へ、-1から再び0へと変わります。このサイクルが繰り返されることで、滑らかな波の形になります。
この周期的な性質を利用して、sin() 関数を使うことで、波の動きや振動を表現することができます。画面上でこれを視覚化すると、ちょうど波線のように見えます。
時計の針が12時の位置（真上）にあるとき、それが「1」の位置。これは、サイン関数の最大値を意味しています。
例えば、時計の針が3時の位置（右側）にあるとき、針は「0」の位置にある。この「0」というのは、サイン関数が波の中心にいることを示しています。
そして、6時の位置（真下）に来ると、針は「-1」の位置に。これは、サイン関数が最小値に達したことを意味しています。
このように、針が時計の周りを一周するたびに、サイン関数の値は1から0、そして-1に変わり、また0に戻る。これをグラフにすると、上がったり下がったりする波のように見えるんだよ。だから、サイン関数はこの点の動きを表していて、それが0から1、そして0から-1に繰り返し変わることになる
sin() 関数は三角関数と呼ばれるものの一部で、円の周りを回る点のY座標を計算するものです。直感的に言うと、これが波の動きの元になっています。
円の周りを回る点を考えてみてください。その点の位置を角度（ラジアン）で表します。角度が増えると、点は円を回り続けます。この点の上下の動き（Y座標）が sin() 関数によって計算されるものです。
だから、角度が0から360度に一周するとき、Y座標は円の上半分から始まり、次に下半分に移動し、再び上半分に戻ってくる。この動きが -1 から 1 への振れ幅を生み出します。そして、それが繰り返されることで波の形ができるのです。
要するに、sin() 関数は円の周りを回る点のY方向の動きを使って、波のような動きを作るということ。
もう少し簡単に説明。
大きな丸い時計があるとします。この時計の周りを小さな点がぐるぐる回っています。その点がどこにあるかを調べるために、時計の中心からその点まで線を引く。この線を「角度」って呼ぶ。
この点が一番上に来るとき、線はまっすぐ上に伸びているから、点は「1」の位置にあることになる。反対に、一番下に来るとき、点は「-1」の位置にある。そして、一番左や一番右に来るときは「0」の位置にある。
この点が時計の周りをぐるぐる回ることで、上に行ったり下に行ったりする。これが波のように見えるのは、この動きをグラフに描いたときに、上に行ったり下に行ったりするラインになるから。
だから、サイン関数はこの点の動きを表していて、それが0から1、そして0から-1に繰り返し変わる。
【Processing】sin()関数はどんな表現で使えそうか
上下に揺れる波や音を表現をするときに役に立ちます。
【Processing】sin()関数を使ってみた感想
なぜ波線が描けるのか、なぜ0、1、-1なのかを理解するのにかなり時間がかかりました。
今回の記事の中で書いている構文は、定期的に復習するために印刷をしました。
特にforループとsin(angle)の数式の組み合わせがかなりややこしかったので、もう少し早く理解できるようになりたいです。
ワタタクそれでは今日もレッツワクワクコーディング。